The discovery of x-ray diffration by crystals, properties of crystals and electrons in crystals has opened up an amazing fields of study. A crystal is formed by adding atoms in a constant environment.
Basis
The crystal structure is formed by adding more and more basis to every lattice point as you see below. The lattice in three dimensions may be defined by the three translation vectors $\textbf{a}_1,\textbf{a}_2,\textbf{a}_3$.
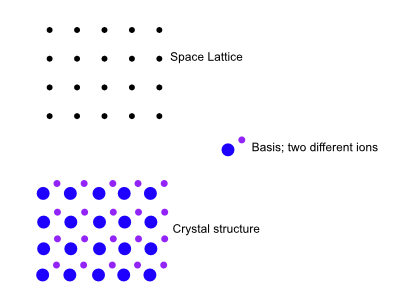
Once the crystal axes have been chosen, the basis of the structure can be indentified. The lattice points are just a mathematical abstraction. An important variable here is the position of the center of an atom $j$ of the basis relative to the associated lattice point.
$\textbf{r}_j = x_j\textbf{a}_1 + y_j\textbf{a}_2 + z_j\textbf{a}_3$
Primitive Lattice Cell
The second thing you need to think about after the primitive axes is the primitive cell. The figure below shows the parallelepiped definded by the primitive axes $\textbf{a}_1,\textbf{a}_2,\textbf{a}_3$ is called the primitive cell.
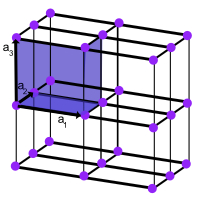Primitive cell of space lattice in three dimensions
Lattice Translation Vectors
A perfect crystal is constructed by an infinite repetition of identical groups of atoms (basis) attched to the set of mathematical points (lattice). The three dimensional vectors $\textbf{a}_1,\textbf{a}_2,\textbf{a}_3$ are chosen such that the arrangement of atoms in the crystal looks the same when viewed from the point $\textbf{r}$ as when viewed from every point $\textbf{r}^\prime$ translated by an integral multiple of the $\textbf{a}$s:
$\textbf{r}^\prime = \textbf{r} + u_1\textbf{a}_1 + u_2\textbf{a}_2 + u_3\textbf{a}_3$
Here $u_1,u_2,u_3$ are any arbitrary integers. The lattice is said to be primitive if any two points from which the atomic arrangement looks the same with suitable choice of the intergers $u_i$. We have the primitive translation vectors $a_i$ if there is no cell that is smaller volume than $\textbf{a}_1 \cdot \textbf{a}_2 \times \textbf{a}_3$ that can serve as a building block for the crystal structure. The primitive translation vectors $a_i$ are often used to define the crystal axes. The volume of a parallelepiped with axes $\textbf{a}_1,\textbf{a}_2,\textbf{a}_3$
$V_c = \lvert \textbf{a}_1 \cdot \textbf{a}_2 \times \textbf{a}_3 \rvert$.
Fundamental Types of Lattices
Lattice can be carried into itself by the lattice translations and symmetry operations. Lattice can be found in one, two, three, four and six fold rotation axes carry the lattice into itself, corresponding to rotations by $2\pi$, $\pi$, $\frac{2\pi}{3}$, $\frac{\pi}{2}$,$\frac{\pi}{3}$ radians and by intergral multiples of these rotations. You can think of these rotations as $\frac{2\pi}{1}$, $\frac{2\pi}{2}$, $\frac{2\pi}{3}$, $\frac{2\pi}{4}$,$\frac{2\pi}{6}$, these fractions of $2\pi$ are the reason why we will flip everything later on and work with the reciprocal lattice.
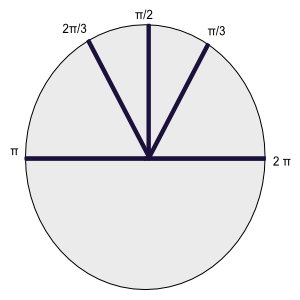
Two-Dimensional Lattice Types
A general lattice is invariant only under rotation of $\pi$ and $2\pi$ about any lattice point. Special lattice of the oblique type can be invariant under rotation of $2\pi/3$, $\pi/2$, $\pi/3$ or under mirror reflection.
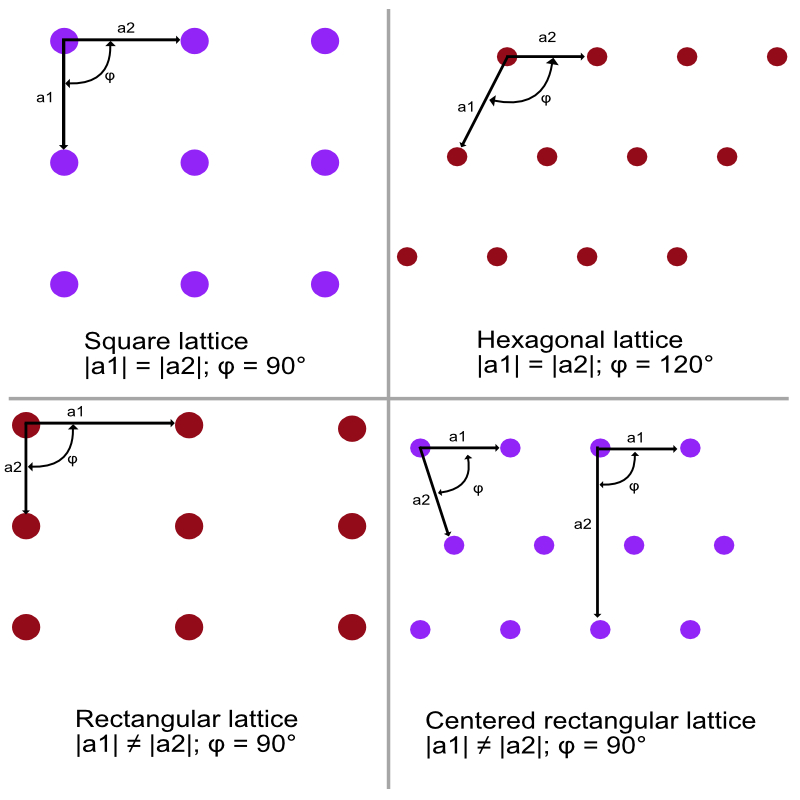
There are four types of 2D lattice, this number comes from the fact that we need to have restrictions on $\textbf{a}_1$ and $\textbf{a}_2$. We need to impose restrictive conditions on $\textbf{a}_1$ and $\textbf{a}_2$ if we want to construct a lattice that will be invariant under rotation of $2\pi/3$, $\pi/2$, $\pi/3$. With the oblique type we have five types of 2d lattice, they are called the Bravais lattice.
Three-Dimensional Lattice Types
Now the conditions of invariant gets a little more complicated in three-dimenstions. There are 14 lattice types in 3D. Let’s us list them in this table:
| System | Number of littace types | Restrictions on conventional cell axes and angles |
|---|---|---|
| Triclinic | 1 | $\textbf{a}_1 \neq \textbf{a}_2 \neq \textbf{a}_3$ $\alpha \neq \beta \neq \gamma$ |
| Monoclinic | 2 | $\textbf{a}_1 \neq \textbf{a}_2 \neq \textbf{a}_3$ $\alpha = \gamma = 90^{\circ} \neq \beta$ |
| Orthorhombic | 4 | $\textbf{a}_1 \neq \textbf{a}_2 \neq \textbf{a}_3$ $\alpha = \beta = \gamma = 90^{\circ}$ |
| Tetragonal | 2 | $\textbf{a}_1 = \textbf{a}_2 \neq \textbf{a}_3$ $\alpha = \beta = \gamma = 90^{\circ}$ |
| Cubic* | 3 | $\textbf{a}_1 = \textbf{a}_2 = \textbf{a}_3$ $\alpha = \beta = \gamma = 90^{\circ}$ |
| Trigonal | 1 | $\textbf{a}_1 = \textbf{a}_2 = \textbf{a}_3$ $\alpha = \beta = \gamma < 120^{\circ}, \neq 90^{\circ}$ |
| Hexagonal | 1 | $\textbf{a}_1 = \textbf{a}_2 \neq \textbf{a}_3$ $\alpha = \beta = 90^{\circ} \gamma = 120^{\circ}$ |
The general lattice is triclinic and the rest are special lattice in seven types of cells.
*The cubic lattic is shown below, there are three types of lattice in the cubic system; the simple lattice (sc), body-centered cubic (bcc) and face-centered lattice (fcc).
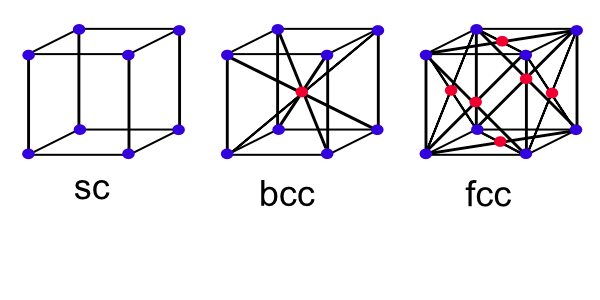
The characteristics of the cubic lattice are summarized in the below table:
| Simple | Body-centered | Face-centered | |
|---|---|---|---|
| Volume, conventional cell | $a^3$ | $a^3$ | $a^3$ |
| Lattice points per cell | 1 | 2 | 4 |
| Volume, primitive cell | $a^3$ | $\frac{1}{2}a^3$ | $\frac{1}{4}a^3$ |
| Lattice points per unit volume | $\frac{1}{a^3}$ | $\frac{2}{a^3}$ | $\frac{4}{a^3}$ |
| Number of nearest neighbors | 6 | 8 | 12 |
| Nearest neighbor distance | $a$ | $\sqrt{3}\frac{a}{2}$ | $\frac{a}{\sqrt{2}}$ |
| Number of second neighbors | 12 | 6 | 6 |
| Second neighbor distance | $\sqrt{2}a$ | $a$ | $a$ |
| Packing fraction* | $\frac{1}{6}\pi$ | $\frac{1}{8}\pi\sqrt{3}$ | $\frac{1}{6}\pi\sqrt{2}$ |
*The packing fraction is the maximum proportion of the available volume that can be filled with hard spheres.
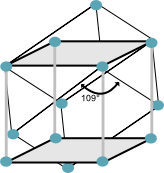
The primitive cell of the bcc is shown below. The rhombohedron cell of edge $\frac{1}{2}\sqrt{3}a$ and the angle between adjacent edges is $109^{\circ}$.
The primitive translation vectors of the bcc are shown below:
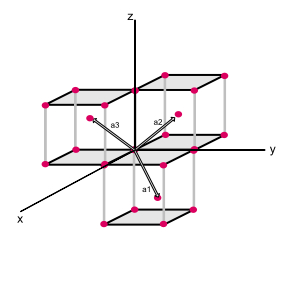
Primitive translation vectors of the body-centered cubic lattice, these vectors connect the lattice point at the origin to lattice points at the body centers. In terms of the cude adge angle $a$, the primitive translation vectors are
$\textbf{a}_1 = \frac{1}{2}a(\hat{x} + \hat{y} - \hat{z})$
$\textbf{a}_2 = \frac{1}{2}a(-\hat{x} + \hat{y} + \hat{z})$
$\textbf{a}_3 = \frac{1}{2}a(\hat{x} - \hat{y} + \hat{z})$
$\hat{x}, \hat{y}$ and $\hat{z}$ are the Cartesian unit vectors.
The primitive translation vectors of the fcc lattice are shown below
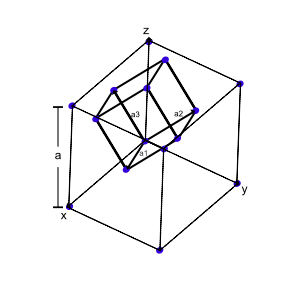
The rhombohedral primitive cell of the fcc, the primitive translation vectors $\textbf{a}_1, \textbf{a}_2, \textbf{a}_3$ connect the lattice point at the origin with lattice points at the face centers. The primitive translation vectors are:
$\textbf{a}_1 = \frac{1}{2}a(\hat{x}+\hat{y})$
$\textbf{a}_2 = \frac{1}{2}a(\hat{y}+\hat{z})$
$\textbf{a}_3 = \frac{1}{2}a(\hat{z}+\hat{x})$
and the angles between the axes are $60^{\circ}$.
Sodium Chloride Structure
The sodium chloride, NaCl structure is a face-centered cubic; the basis consists of one Na+ ion and one Cl- ion as shown below:
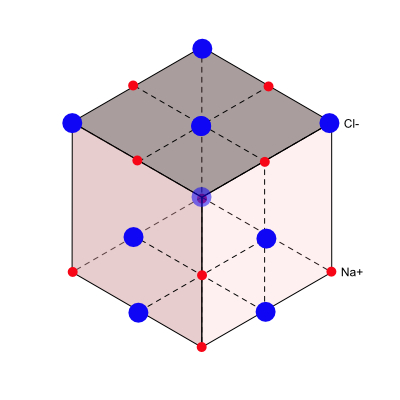
Every lattice point ion in the NaCl structure has six brother ions of the other type.
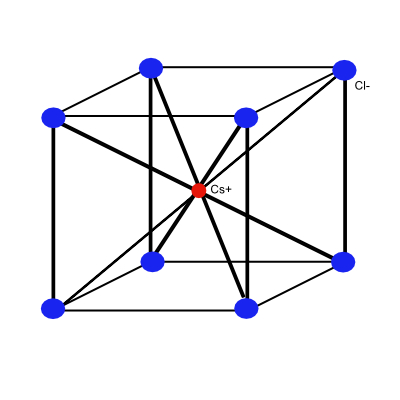
Cesium Chloride Structure
The cesium chloride structure, CsCl is shown below, there is one molecule per primitivecell. Each atom may be viewed as at the center of a cube of atoms of the opposite kind, so that the number of the nearest neighbors is eight.
Cubic Zinc Sulfide Structure
The cubic zinc sulfide structure results when Zn atoms are placed on one fcc lattice and S atoms on the other fcc lattice as shown below.
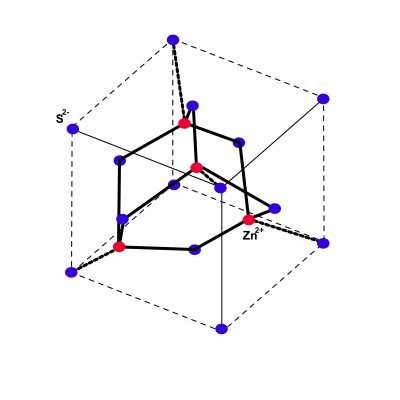
There are four molecules of ZnS per conventional cell. About each atom there are four equally distant atoms of the opposite king arranged at the corners of a regular tetrahedron.
Diamond Structure
The final strcuture we have is the diamond, the diamond structure is that of the semiconductors silicon and germanium and is related to the structure of sevral important semiconductor binary compounds.
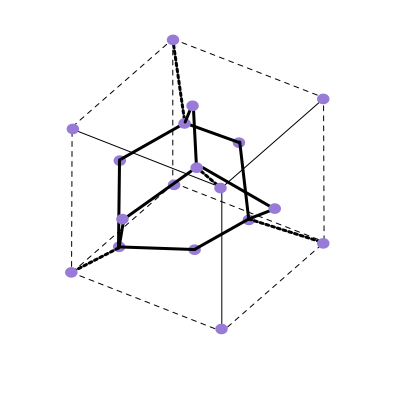
The space lattice of diamond is fcc. Each atom has 4 nearest neighbors and 12 next nearest neighbors.
Crystal Structure of the Elements
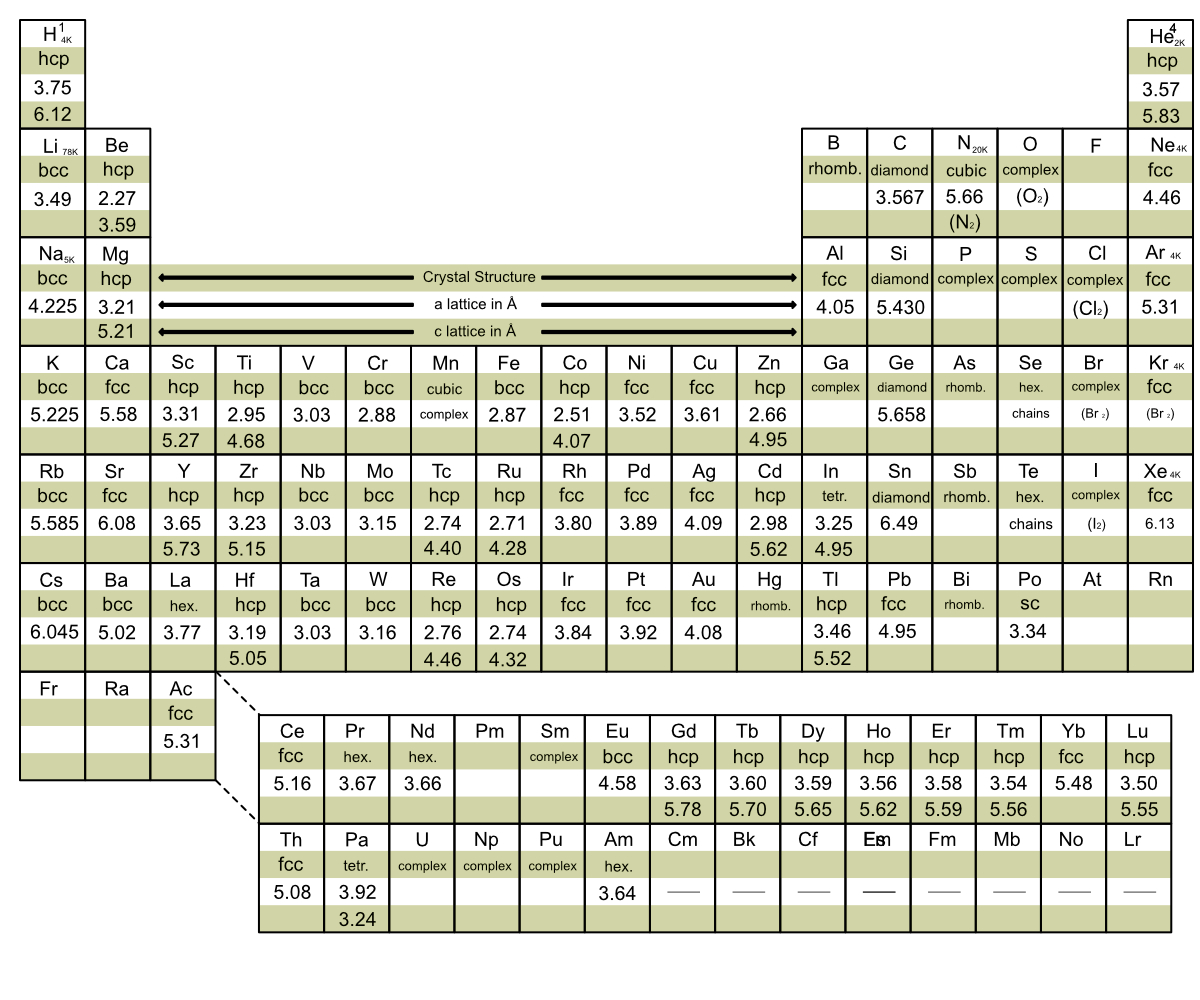
Note: This work is done using Introduction to Solid State Physics by Charles Kittel